A matrix may be classified by types. It is possible for a matrix to belong to more than one type.
- A row matrix is a matrix with only one row.
E is a row matrix of order 1 × 1
B is a row matrix of order 1 × 3
- A column matrix is a matrix with only one column.
C is a column matrix of order 1 × 1
D is a column matrix of order 2 × 1
A column matrix of order 2 ×1 is also called a vector matrix.
- A zero matrix or a null matrix is a matrix that has all its elements zero.
O is a zero matrix of order 2 × 3
- A square matrix is a matrix with an equal number of rows and columns.
T is a square matrix of order 2 × 2
V is a square matrix of order 3 × 3
- A diagonal matrix is a square matrix that has all its elements zero except for those in the diagonal from top left to bottom right; which is known as the leading diagonal of the matrix.
B is a diagonal matrix
- A unit matrix is a diagonal matrix whose elements in the diagonal are all ones.
P is a unit matrix.
In linear algebra, a matrix is in echelon form if it has the shape resulting of a Gaussian elimination. Row echelon form means that Gaussian elimination has operated on the rows and column echelon form means that Gaussian elimination has operated on the columns. In other words, a matrix is in column echelon form if its transpose is in row echelon form. Therefore only row echelon forms are considered in the remainder of this article. The similar properties of column echelon form are easily deduced by transposing all the matrices.
Specifically, a matrix is in row echelon form if
All nonzero rows (rows with at least one nonzero element) are above any rows of all zeroes (all zero rows, if any, belong at the bottom of the matrix).
The leading coefficient (the first nonzero number from the left, also called the pivot) of a nonzero row is always strictly to the right of the leading coefficient of the row above it (some texts add the condition that the leading coefficient must be 1.)
All entries in a column below a leading entry are zeroes (implied by the first two criteria).
This is an example of a 3×5 matrix in row echelon form:

Reduced row echelon form
A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions:
It is in row echelon form.
Every leading coefficient is 1 and is the only nonzero entry in its column.
The reduced row echelon form of a matrix may be computed by Gauss–Jordan elimination. Unlike the row echelon form, the reduced row echelon form of a matrix is unique and does not depend on the algorithm used to compute it.
This is an example of a matrix in reduced row echelon form:

Note that this does not always mean that the left of the matrix will be an identity matrix, as this example shows.
For matrices with integer coefficients, the Hermite normal form is a row echelon form that may be computed using Euclidean division and without introducing any rational number nor denominator. On the other hand, the reduced echelon form of a matrix with integer coefficients generally contains non-integer entries.
Transformation to row echelon form
By means of a finite sequence of elementary row operations, called Gaussian elimination, any matrix can be transformed to row echelon form. Since elementary row operations preserve the row space of the matrix, the row space of the row echelon form is the same as that of the original matrix.
The resulting echelon form is not unique; for example, any multiple by a scalar of a matrix in echelon form is also an echelon form of the same matrix. However, every matrix has a unique reduced row echelon form. This means that the nonzero rows of the reduced row echelon form are the unique reduced row echelon generating set for the row space of the original matrix.
Systems of linear equations
A system of linear equations is said to be in row echelon form if its augmented matrix is in row echelon form. Similarly, a system of equations is said to be in reduced row echelon form or canonical form if its augmented matrix is in reduced row echelon form.
The canonical form may be viewed as an explicit solution of the linear system. In fact, the system is inconsistent, if and only if one of the equations of the canonical form is reduced to 1 = 0. Otherwise, regrouping in the right hand side all the terms of the equations, but the leading ones expresses the variables corresponding to the pivots as constants or linear functions of the other variables, if any.
Matrix (mathematics)
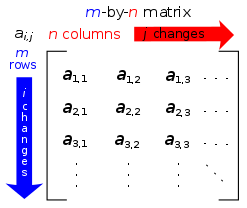
Each element of a matrix is often denoted by a variable with two subscripts. For instance, a2,1 represents the element at the second row and first column of a matrixA.
- A matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.The individual items in a matrix are called its elements or entries. An example of a matrix with 2 rows and 3 columns is -->
- Matrices of the same size can be added or subtracted element by element. But the rule for matrix multiplication is that two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second. A major application of matrices is to represent linear transformations, that is, generalizations of linear functions such as f(x) = 4x. For example, the rotation of vectors in three dimensional space is a linear transformation which can be represented by a rotation matrix R. If v is a column vector (a matrix with only one column) describing the position of a point in space, the product Rv is a column vector describing the position of that point after a rotation. The product of two matrices is a matrix that represents the composition of two linear transformations. Another application of matrices is in the solution of a system of linear equations. If the matrix is square, it is possible to deduce some of its properties by computing its determinant. For example, a square matrix has an inverse if and only if its determinant is not zero. Eigenvalues and eigenvectors provide insight into the geometry of linear transformations.
Applications of matrices are found in most scientific fields. In every branch of physics, including classical mechanics, optics, electromagnetism, quantum mechanics, and quantum electrodynamics, they are used to study physical phenomena, such as the motion of rigid bodies. In computer graphics, they are used to project a 3-dimensional image onto a 2-dimensional screen. In probability theory and statistics, stochastic matrices are used to describe sets of probabilities; for instance, they are used within the PageRank algorithm that ranks the pages in a Google search.[4] Matrix calculus generalizes classical analytical notions such as derivatives and exponentials to higher dimensions.
A major branch of numerical analysis is devoted to the development of efficient algorithms for matrix computations, a subject that is centuries old and is today an expanding area of research. Matrix decomposition methods simplify computations, both theoretically and practically. Algorithms that are tailored to particular matrix structures, such as sparse matrices and near-diagonal matrices, expedite computations in finite element method and other computations. Infinite matrices occur in planetary theory and in atomic theory. A simple example of an infinite matrix is the matrix representing the derivative operator, which acts on the Taylor series of a function.
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It is the study of lines, planes, and subspaces and their intersections using algebra. Linear algebra assigns vectors as the coordinates of points in a space, so that operations on the vectors define operations on the points in the space.
The set of points with coordinates that satisfy a linear equation form a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in Linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.
Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations.Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations. Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences(particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear ones.
Howdy folks!
Let me tell you some things about me first.
i am 15 years old. I'm currently studying as a 4th year high school student at Regional Science High School III. I was born on the 7th of May, 1999. I was born at Riyadh, Saudi Arabia, but hey! i'm a filipino. haha. My mom is working as an overseas worker at Hong Kong, and my dad is... deceased? hahaha. I have a pet cat, his name is Charing (silly right? my mom is the one responsible for his name :P). I love rock bands namely, Paramore, Fall out boy, All time Low, Linkin Park, and ughh... many many more! haha. i love the color Black and i dislike the color Pink. Let me tell you this story, back then when i was young, i used to love pink 'cause it's so cute and girly. But now that i have come to my senses and now that i have developed a liking for cool stuffs, i started to love the color Black.
I love watching animes and reading mangas, people call us 'Otaku'. I am also infatuated with a very famous youtuber and gamer known as Pewdiepie! I looooove him so much. i love his face, his vids, his humor, EVERYTHING. I am an average student to be honest. I used to be an outstanding student back in grade school i don't know what happened now. hahaha. I can draw, but i'm a terrible dancer haha. I used to play the piano before, but now i forgot how to play it. haha. Sooo yeah, that's basically it. Hope you learned something about me. That's all. Thank you! Tune in for more educational posts. Don't forget to follow! :))


